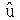 i丂亖倄i 亅丂乮
i丂亖倄i 亅丂乮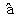 丂亄丂
丂亄丂 倃i乯
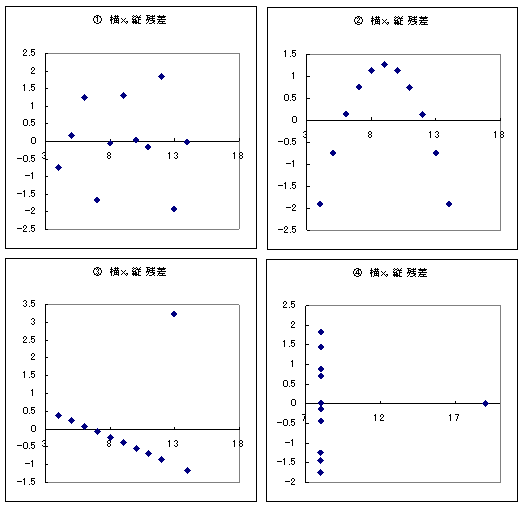
倃i乯丂俀寧俁擔偐傜俆擔傑偱丄嶰塝僙儈僫乕僴僂僗偱僛儈崌廻傪偟傑偟偨丅偐側傝慜偵懖嬈偟偨奆偝傫偼偛懚偠側偄偲巚偄傑偡偑丄朄惌戝妛偵偼僙儈僫乕僴僂僗偑俁偮偁傝傑偡丅壨岥屛嬤偔偵偁傞晉巑僙儈僫乕僴僂僗丄愇壀塣摦応偵暪愝偝傟偨僙儈僫乕僴僂僗偵丄嶰塝偱偡丅嫗媫嶰塝奀娸墂偐傜侾俆暘傎偳偺偲偙傠偵偁傝傑偡丅奀娸偵偼嬤偄偺偱偡偑丄偦傟埲奜偵偼梀傇偲偙傠偑壗傕側偄偺偱丄曌嫮偺弔崌廻偵偼偆偭偰偮偗偱偡丅
丂崱夞偼丄寁検宱嵪妛傪島媊偡傞偙偲偵偟傑偟偨丅偙偺係寧偐傜僛儈偵擖傞俀擭惗丄僛儈偱昁梫側偺偵巹偺扴摉偺寁検宱塩暘愅傪偲傜側偄俁擭惗丄偦傟偵摑寁妛傪儅僗僞乕偟偰偄側偄懖嬈娫嬤偺係擭惗丄寁俀俇柤偑嶲壛偟傑偟偨丅
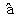 傪丄倐 偺悇掕抣偲偟偰
傪丄倐 偺悇掕抣偲偟偰  傪戙擖偡傞側傜偽丄岆嵎崁偺悇掕抣乮巆嵎乯
傪戙擖偡傞側傜偽丄岆嵎崁偺悇掕抣乮巆嵎乯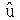 i 偲偟偰
i 偲偟偰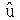 i丂亖倄i 亅丂乮
i丂亖倄i 亅丂乮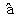 丂亄丂
丂亄丂 倃i乯
倃i乯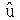 i 偑彫偝偔側傞傛偆偵僷儔儊乕僞偺悇掕抣傪媮傔傑偟傚偆丅偲偄偭偰傕丄巆嵎偼
i 偑彫偝偔側傞傛偆偵僷儔儊乕僞偺悇掕抣傪媮傔傑偟傚偆丅偲偄偭偰傕丄巆嵎偼 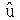 1 偐傜
1 偐傜 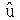 n 傑偱丄値屄偁傝傑偡丅偟偨偑偭偰丄値屄偺慡懱傪彫偝偔偡傞偙偲傪峫偊傑偡丅巆嵎偵偼僾儔僗丄儅僀僫僗偑偁傞偺偱丄扨弮偵懌偟偰偟傑偆偲丄憡嶦偝傟偰僛儘偵嬤偔側傝傑偡丅偦偙偱巆嵎傪偡傋偰僾儔僗偵偟偰懌偡偺偱偡偑丄偦偺偝偄俀忔偟偰僾儔僗偵偟傑偡丅偡側傢偪丄
n 傑偱丄値屄偁傝傑偡丅偟偨偑偭偰丄値屄偺慡懱傪彫偝偔偡傞偙偲傪峫偊傑偡丅巆嵎偵偼僾儔僗丄儅僀僫僗偑偁傞偺偱丄扨弮偵懌偟偰偟傑偆偲丄憡嶦偝傟偰僛儘偵嬤偔側傝傑偡丅偦偙偱巆嵎傪偡傋偰僾儔僗偵偟偰懌偡偺偱偡偑丄偦偺偝偄俀忔偟偰僾儔僗偵偟傑偡丅偡側傢偪丄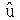 12 亄丒丒丒亄
12 亄丒丒丒亄 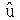 n2
n2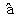 丄
丄 傪媮傔傑偡丅偙傟偐傜媮傔偨 倎丄倐 偺悇掕検
傪媮傔傑偡丅偙傟偐傜媮傔偨 倎丄倐 偺悇掕検 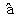 丄
丄 傪嵟彫俀忔悇掕検偲偄偄傑偡丅偡側傢偪丄巆嵎偺俀忔傪嵟彫偵偡傞傛偆偵偟偰媮傔偨悇掕検偲偄偆堄枴偱偡丅
傪嵟彫俀忔悇掕検偲偄偄傑偡丅偡側傢偪丄巆嵎偺俀忔傪嵟彫偵偡傞傛偆偵偟偰媮傔偨悇掕検偲偄偆堄枴偱偡丅 亖俽XY乛俽XX丂丂
亖俽XY乛俽XX丂丂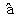 亖
亖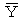 亅
亅
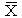
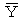 偼僒儞僾儖値屄偐傜側傞倄偺暯嬒丄
偼僒儞僾儖値屄偐傜側傞倄偺暯嬒丄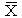 偼倃偺暯嬒偱偡丅晛捠丄暯嬒偼倃偲偐倄偺忋偵僶乕傪偮偗偰昞偟傑偡丅偮偄偱偵尵偊偽丄悇掕検偼忋偵僴僢僩乮丱乯傪偮偗偰昞尰偟傑偡丅
偼倃偺暯嬒偱偡丅晛捠丄暯嬒偼倃偲偐倄偺忋偵僶乕傪偮偗偰昞偟傑偡丅偮偄偱偵尵偊偽丄悇掕検偼忋偵僴僢僩乮丱乯傪偮偗偰昞尰偟傑偡丅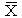 )(倄i亅
)(倄i亅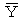 )傪堄枴偟傑偡丅俽XX 偼倃偺曄摦偱丄嚁(倃i亅
)傪堄枴偟傑偡丅俽XX 偼倃偺曄摦偱丄嚁(倃i亅 )2 偱偡丅曄摦傪乮値亅侾乯偱妱傟偽昗杮偺暘嶶傪丄嫟曄摦偺偲偒偼嫟暘嶶傪昞偟傑偡丅偟偨偑偭偰丄倃偺曄摦偼丄倃偺偽傜偮偒傪昞偡偲峫偊偰傛偄偱偟傚偆丅
)2 偱偡丅曄摦傪乮値亅侾乯偱妱傟偽昗杮偺暘嶶傪丄嫟曄摦偺偲偒偼嫟暘嶶傪昞偟傑偡丅偟偨偑偭偰丄倃偺曄摦偼丄倃偺偽傜偮偒傪昞偡偲峫偊偰傛偄偱偟傚偆丅 傪偲傝偁偘傑偟傚偆丅
傪偲傝偁偘傑偟傚偆丅 偼値慻偺倃丄倄偐傜側傞娭悢偱偡丅倃偼旕妋棪曄悢偱偡偑丄倄偼妋棪曄悢偱偡丅偟偨偑偭偰丄
偼値慻偺倃丄倄偐傜側傞娭悢偱偡丅倃偼旕妋棪曄悢偱偡偑丄倄偼妋棪曄悢偱偡丅偟偨偑偭偰丄 傕妋棪曄悢偵側傝傑偡丅
傕妋棪曄悢偵側傝傑偡丅 傪寁嶼偡傟偽丄
傪寁嶼偡傟偽丄 偼傂偲偮偺妋掕偟偨抣偵側傝傑偡丅偟偐偟丄偄傑偼娤應抣傪摼傞慜偵丄悇掕偡傞巇慻傒傪嶌偭偰偍偒偨偄偺偱偡丅偟偨偑偭偰丄倃丄倄偺抣偼傢偐偭偰偄傑偣傫丅偲偄偆傢偗偱丄
偼傂偲偮偺妋掕偟偨抣偵側傝傑偡丅偟偐偟丄偄傑偼娤應抣傪摼傞慜偵丄悇掕偡傞巇慻傒傪嶌偭偰偍偒偨偄偺偱偡丅偟偨偑偭偰丄倃丄倄偺抣偼傢偐偭偰偄傑偣傫丅偲偄偆傢偗偱丄 偺抣傕掕傑偭偰偼偄傑偣傫丅
偺抣傕掕傑偭偰偼偄傑偣傫丅 偼倃丄倄偺娭悢側偺偱丄偦偺暘晍偼俁偮偺僷儔儊乕僞偲丄値屄偺倃偺抣偑傢偐傟偽寛傑偭偰偔傞妋棪曄悢偲偄偆偙偲偵側傝傑偡丅
偼倃丄倄偺娭悢側偺偱丄偦偺暘晍偼俁偮偺僷儔儊乕僞偲丄値屄偺倃偺抣偑傢偐傟偽寛傑偭偰偔傞妋棪曄悢偲偄偆偙偲偵側傝傑偡丅 偺暘晍偱偡偑丅
偺暘晍偱偡偑丅 偺娭悢傪曄宍偡傟偽丄倄1丆丒丒丒丆倄n 偺堦師寢崌偱昞偣傞偙偲偑傢偐傝傑偡丅堦師寢崌偲偄偆偙偲偑傢偐傜側偄傫偱偟傚偆両
偺娭悢傪曄宍偡傟偽丄倄1丆丒丒丒丆倄n 偺堦師寢崌偱昞偣傞偙偲偑傢偐傝傑偡丅堦師寢崌偲偄偆偙偲偑傢偐傜側偄傫偱偟傚偆両 偑偙偆昞尰偱偒傞偙偲傪乽慄宍惈乿偲屇傫偱偄傑偡丅
偑偙偆昞尰偱偒傞偙偲傪乽慄宍惈乿偲屇傫偱偄傑偡丅 偼惓婯暘晍傪偡傞丄偲偄偆偙偲偱偡丅
偼惓婯暘晍傪偡傞丄偲偄偆偙偲偱偡丅 偑惓婯暘晍偩偭偨傜丄暯嬒偲暘嶶偑傢偐傟偽偄偄丅
偑惓婯暘晍偩偭偨傜丄暯嬒偲暘嶶偑傢偐傟偽偄偄丅 偺暯嬒丄婜懸抣 俤乮
偺暯嬒丄婜懸抣 俤乮 乯偼丠丂偳偆偭偰偙偲側偔寁嶼偱偒傞偺偩偑丄傒傫側偵偼儉儕丅寢壥偼丄
乯偼丠丂偳偆偭偰偙偲側偔寁嶼偱偒傞偺偩偑丄傒傫側偵偼儉儕丅寢壥偼丄 乯亖丂倐
乯亖丂倐  乯亖冃2乛(側傫偲偐)
乯亖冃2乛(側傫偲偐)  偺(側傫偲偐)偺晹暘偼丄
偺(側傫偲偐)偺晹暘偼丄 偲偼暿偺傕偺偵側傝傑偡丅
偲偼暿偺傕偺偵側傝傑偡丅 偺暘晍偼惓婯暘晍偱丄暯嬒偑僷儔儊乕僞倐偵堦抳偟丄暘嶶偼冃2乛(側傫偲偐) 偵側傞丅婰崋偱彂偔偲
偺暘晍偼惓婯暘晍偱丄暯嬒偑僷儔儊乕僞倐偵堦抳偟丄暘嶶偼冃2乛(側傫偲偐) 偵側傞丅婰崋偱彂偔偲 丂乣丂俶乮倐丆冃2乛(側傫偲偐)乯
丂乣丂俶乮倐丆冃2乛(側傫偲偐)乯 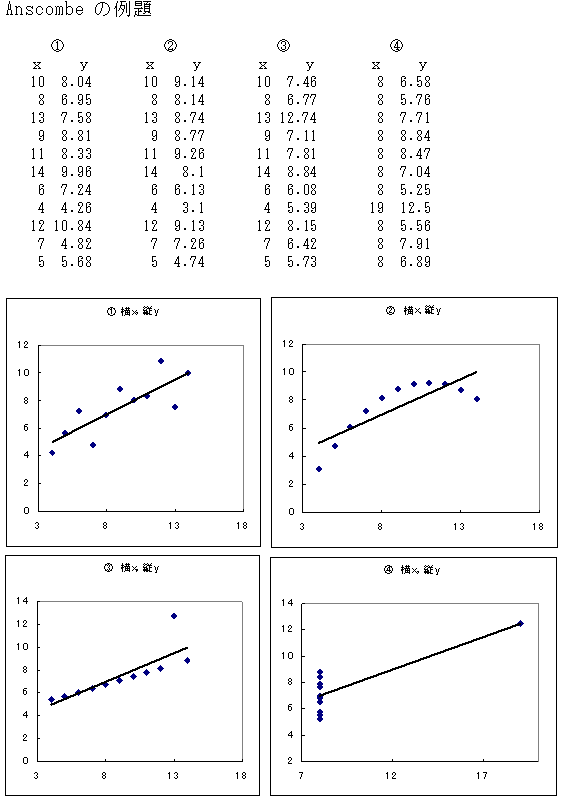
 傪岺晇偟偰嶌傞偺偑帺慠偱偁傠偆丅
傪岺晇偟偰嶌傞偺偑帺慠偱偁傠偆丅 偼偡偱偵弎傋偨傛偆偵
偼偡偱偵弎傋偨傛偆偵 丂乣丂俶乮倐丆冃2乛(側傫偲偐)乯
丂乣丂俶乮倐丆冃2乛(側傫偲偐)乯  偲乮側傫偲偐乯偺晹暘偼僨乕僞偐傜寁嶼偱偒傞偑丄冃偼暘偐傜側偄丅冃偺戙傢傝偵僨乕僞偐傜媮傔偨昗弨岆嵎乮倱乯傪梡偄傞偙偲偵側傞丅昗弨岆嵎偼昗杮暘嶶乮倱2乯偺暯曽崻偱偁傞丅昗杮暘嶶偼丄巆嵎曄摦乮偁傞偄偼巆嵎暯曽榓丄俽俽俼丗Sum of Squared Residual乯傪帺桼搙乮値亅倠亅侾乯偱妱偭偨傕偺偱偁傞丅
偲乮側傫偲偐乯偺晹暘偼僨乕僞偐傜寁嶼偱偒傞偑丄冃偼暘偐傜側偄丅冃偺戙傢傝偵僨乕僞偐傜媮傔偨昗弨岆嵎乮倱乯傪梡偄傞偙偲偵側傞丅昗弨岆嵎偼昗杮暘嶶乮倱2乯偺暯曽崻偱偁傞丅昗杮暘嶶偼丄巆嵎曄摦乮偁傞偄偼巆嵎暯曽榓丄俽俽俼丗Sum of Squared Residual乯傪帺桼搙乮値亅倠亅侾乯偱妱偭偨傕偺偱偁傞丅 亖俽XY乛俽XX 偲側傞偺傪榖偟偨偱偟傚偆丅偦傟傪摉偰偼傔傟偽丄偱偒傞丅偟偐偟丄倳帺恎偼娤應偝傟側偄偺偱丄偦偺悇掕検偱偁傞巆嵎傪戙擖偡傞丅偦傟偑
亖俽XY乛俽XX 偲側傞偺傪榖偟偨偱偟傚偆丅偦傟傪摉偰偼傔傟偽丄偱偒傞丅偟偐偟丄倳帺恎偼娤應偝傟側偄偺偱丄偦偺悇掕検偱偁傞巆嵎傪戙擖偡傞丅偦傟偑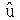 偐傜偱偒偰偄傞偙偲偵傛傞丅俢倂斾偺暘晍傪峫偊傞偺偩偑丄
偐傜偱偒偰偄傞偙偲偵傛傞丅俢倂斾偺暘晍傪峫偊傞偺偩偑丄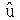 偐傜偱偒偰偄傞偲偄偆偙偲偼丄愢柧曄悢偺娭悢偵側偭偰偄傞偲偄偆偙偲丅偲偄偆偙偲偼丄愢柧曄悢偺偄傠偄傠側抣偵傛偭偰暘晍偑堎側偭偰偔傞丅偟偨偑偭偰丄婞媝堟傕愢柧曄悢偺抣偵傛偭偰堎側偭偰偔傞丅偙傟偱偼悢昞傪嶌傞忋偱傗偭偐偄偩偹丅偩偐傜丄偳傫側愢柧曄悢偺抣偑偒偰傕懳墳偱偒傞悢昞偵偟偰偍偒偨偄丅偨偲偊偽俆亾偺桳堄悈弨偺応崌丄偄傠偄傠側愢柧曄悢偵懳墳偡傞婞媝堟偺偆偪丄傕偭偲傕俀偵嬤偄婞媝堟偺抣乮忋尷乯偲丄傕偭偲傕俀偐傜墦偄婞媝堟乮壓尷乯偑峫偊傜傟傞偱偟傚偆丅偦偺娫偺抣偼丄偳偺愢柧曄悢偺婞媝堟偵懳墳偟偰偄傞偐傢偐傜側偄偺偱敾抐偱偒側偄傛偹丅
偐傜偱偒偰偄傞偲偄偆偙偲偼丄愢柧曄悢偺娭悢偵側偭偰偄傞偲偄偆偙偲丅偲偄偆偙偲偼丄愢柧曄悢偺偄傠偄傠側抣偵傛偭偰暘晍偑堎側偭偰偔傞丅偟偨偑偭偰丄婞媝堟傕愢柧曄悢偺抣偵傛偭偰堎側偭偰偔傞丅偙傟偱偼悢昞傪嶌傞忋偱傗偭偐偄偩偹丅偩偐傜丄偳傫側愢柧曄悢偺抣偑偒偰傕懳墳偱偒傞悢昞偵偟偰偍偒偨偄丅偨偲偊偽俆亾偺桳堄悈弨偺応崌丄偄傠偄傠側愢柧曄悢偵懳墳偡傞婞媝堟偺偆偪丄傕偭偲傕俀偵嬤偄婞媝堟偺抣乮忋尷乯偲丄傕偭偲傕俀偐傜墦偄婞媝堟乮壓尷乯偑峫偊傜傟傞偱偟傚偆丅偦偺娫偺抣偼丄偳偺愢柧曄悢偺婞媝堟偵懳墳偟偰偄傞偐傢偐傜側偄偺偱敾抐偱偒側偄傛偹丅